In the past week, I started an ambitious project. It is to make a vector math library that runs the computations on the GPU. The motivation is to eventually make this into a deep learning framework, and learn the fundamental concepts on a deeper level.

Currently, I have an implementation of n-dimensional arrays that can be added, subtracted, take dot product, and perform matrix multiplication. It’s implemented using C++ and CUDA.

How do you program a GPU?

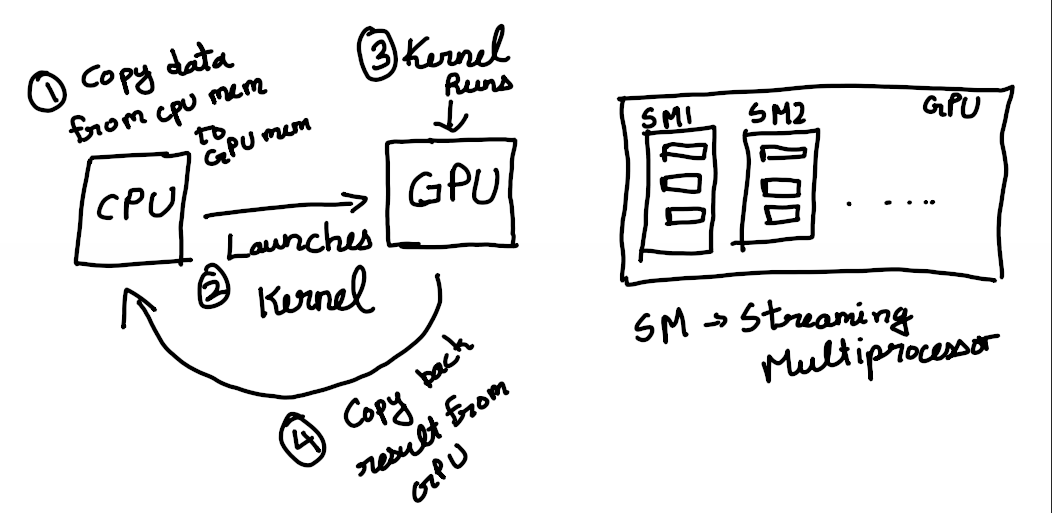
A GPU has thousands of processors grouped into a construct called SM (Streaming Multiprocessor). All these processors can execute a single instruction on different data, at the same time. Hence GPU belongs to the class of SIMD (Single Instruction Multiple Data) Processor.

These processes run in a thread, and threads are grouped into blocks and they are grouped into grids. A function running on the GPU is called a kernel.

So, how do you go about making a program which runs on the GPU? This more or less involves these 4 steps:

1. Copy data from CPU memory to the memory allocated on the GPU
2. Launch a kernel from the CPU specifying how many threads and other details
3. Kernel is executed in the GPU
4. Copy back the result from the GPU

This is just a quick intro to Parallel Programming, I would highly recommend looking into the following playlist by Udacity - https://www.youtube.com/playlist?list=PLAwxTw4SYaPnFKojVQrmyOGFCqHTxfdv2

How did it all go down?

Connecting all the Source Files

I need a way to compile all the .cpp files and .cu files together into an executable. This is exactly why we have Build Systems. I have little experience with CMake, but for this project, I went ahead with Make itself.

(Note: CMake is technically a build system generator, as it generates Makefile)

I never got down to learning about Make, so this proved to be an excellent opportunity to do so.

If you are interested in learning more about Makefiles, the following would prove to be an excellent resource - https://makefiletutorial.com/

Making N-dimensional Arrays in Cpp

I created a class called “ndarray”, which has two members - a data vector and a shape vector. The data vector stores the data in a contiguous fashion and the shape vector holds the dimensions of the ndarray. We use the shape information to access the data vector. That’s pretty much it.

Implementing Vector Addition and Subtraction

This is pretty simple, add the respective elements in individual threads, and thus we would have added all the elements.

__global__ void vectorAdd(float *a, float *b, float *c, int n) {
	int i = blockIdx.x * blockDim.x + threadIdx.x;
	if (i < n) {
		c[i] = a[i] + b[i];
	}
}

We need the if condition to mask off threads whose ID would be greater than the number of elements We could similarly implement subtraction and element-wise multiplication.

Matrix Multiplication

Now, this is one deep rabbit hole. Matrix Multiplication is one of the important operations out there, and there are several optimizations out there. I found an interesting article that goes over a few of the important optimizations - https://siboehm.com/articles/22/CUDA-MMM. I plan on implementing all the stages mentioned in the article. As of now, I have reached the second stage of optimization.

We implement a general version of matrix multiplication called SGEMM - Single Precision General Matrix Multiplication. Let A, B, and C be matrices, then $$ C = \alpha * (A * B) + \beta * C $$ is an SGEMM.

Naive Implementation

So we will have one thread computing the output for one cell in the output matrix. We will launch a grid of blocks and each block will be of size 32 * 32.

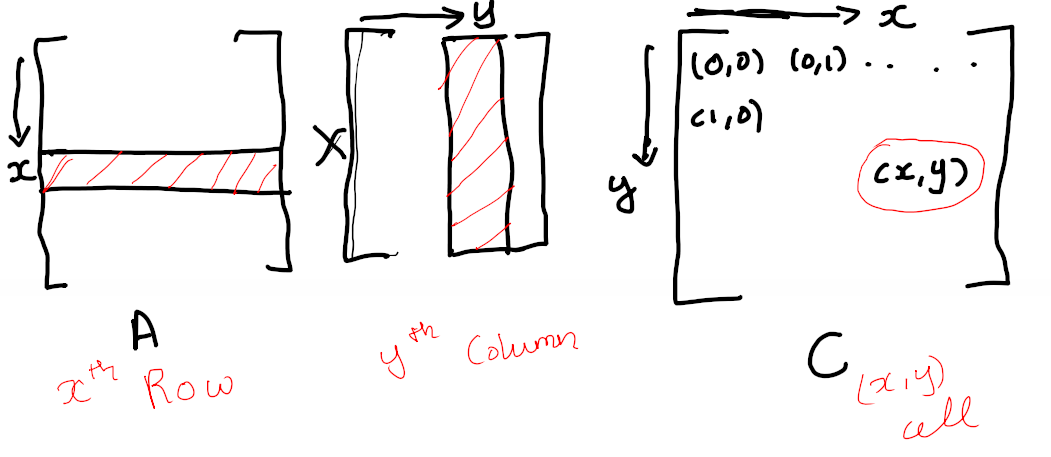
For the (x,y) cell in the output matrix, we will need the x Row from A and the y column from B

__global__ void sgemm_naive(float *a, float *b, float *c, int m, int n, int common_dim, float alpha, float beta){
	const uint COLS = blockIdx.x * blockDim.x + threadIdx.x;
	const uint ROWS = blockIdx.y * blockDim.y + threadIdx.y;
	if (COLS < n && ROWS < m){
		float sum = 0;
		for (int i = 0; i < common_dim; ++i){
			sum += a[ROWS * common_dim + i] * b[i * n + COLS];
		}
		c[ROWS*n + COLS] = alpha * sum + beta * c[ROWS*n + COLS];
	}
}

For multiplying a 128x128 matrix with a 128x256 matrix, it took 1.35 seconds. Now let’s try to make it faster.

Coalescence Access to Global Memory

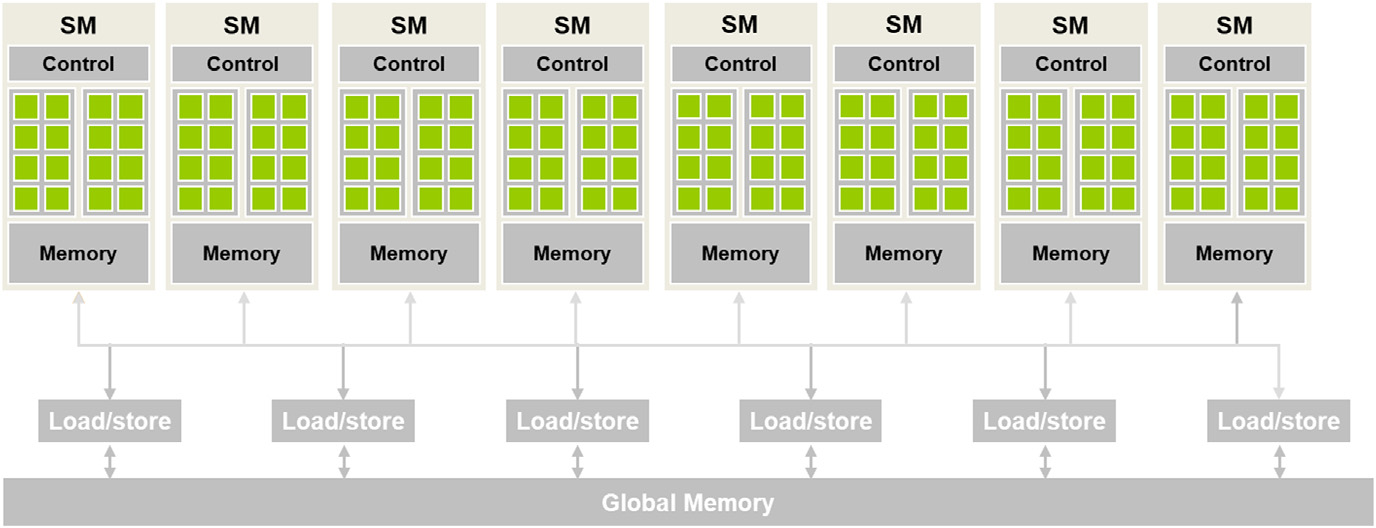
(Source - Book - Programming Massively Parallel Processors by Wen-Mei, David B.Kirk)

The above is the architecture for a CUDA-capable GPU. Each thread has its memory, and each SM will have a shared memory, accessible to all the threads in the particular SM. All the threads will have access to Global Memory.

Once a block is set to execute in an SM, it is partitioned into warps. A warp contains 32 threads. Consecutive memory access by threads in the same warp can be executed with a single LOAD instruction. We are going to exploit this property to improve our kernel.

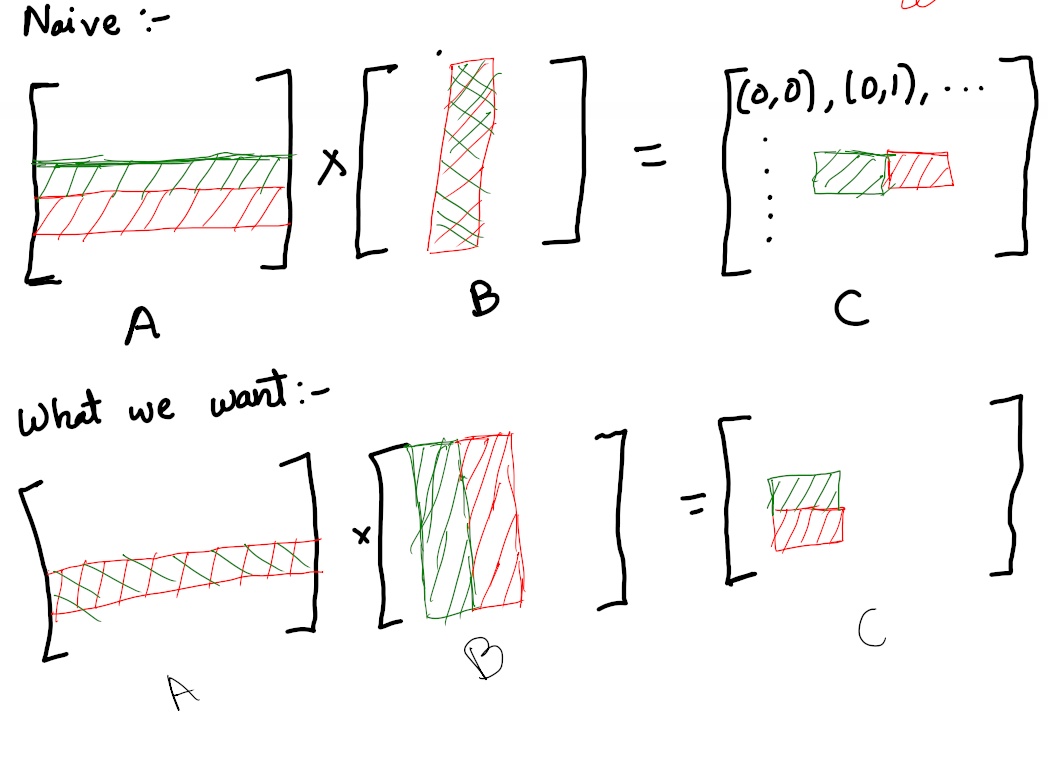
Let’s assume, the threads responsible for the green and red cells are grouped in the same warp. So In our naive implementation, both those cells would want that column from B, but it is not consecutive, so we cannot load it at once.

However, let’s assume, we got the green and red cells in the bottom matrix running on the consecutive threads. Then, both will require that common row of A, which is consecutive and hence can be loaded using one load instruction.

Thus, we have

__global__ void sgemm_coalescene(float *a, float *b, float *c, int m, int n, int common_dim, float alpha, float beta){
	const uint BlockSize = 32;
	const uint COLS = blockIdx.x * BlockSize + threadIdx.x % BlockSize;
	const uint ROWS = blockIdx.y * BlockSize + threadIdx.x / BlockSize;
	if (COLS < n && ROWS < m){
		float sum = 0;
		for (int i = 0; i < common_dim; ++i){
			sum += a[ROWS * common_dim + i] * b[i * n + COLS];
		}
		c[ROWS*n + COLS] = alpha * sum + beta * c[ROWS*n + COLS];
	}
}

We have to make our block one-dimensional but still hold the same number of threads.

Once we do this, we could multiply 128x128 with a 128x256 matrix in 1.12 seconds.

This is where I am right now, but I could optimize this a lot more, and that’s what I plan on doing next week.

Code - https://github.com/KarthikSundar2002/CUDAmath

To learn more about programming GPUs, read the book “Programming Massively Parallel Processors” and look into the course mentioned above.