Attention Mechanisms

The original self-attention has a quadratic complexity with sequence length. To overcome this quadratic complexity, there have been several attempts

Longformer

Introduced in [1]
Combines local-windowed attention and a task-specific global attention.

The earlier attempts where to just convert long sequences into shorter ones falling within BERT limit. (You can read about BERT in RNNs to GPT and BERT)

It uses a fixed size window attention surrounding each token. When stacked, it's receptive field increases, similar to that of convolution.

Similar to Dilated Convolutions, the window could be dilated as well, increasing the receptive field. The authors found that it is better to use dilation in few heads in multi-head attention. The intuition being that some could focus on local context and while others could attend to those tokens which are farther.

In BERT, we had a few task specific tokens like [CLS] token. To allow the model to learn task specific representations, some tokens attend to every token in the sequence and every token attends to it.

For Classification, [CLS] token has global attention
For Question Answering, All the Question Tokens have Global Attention.

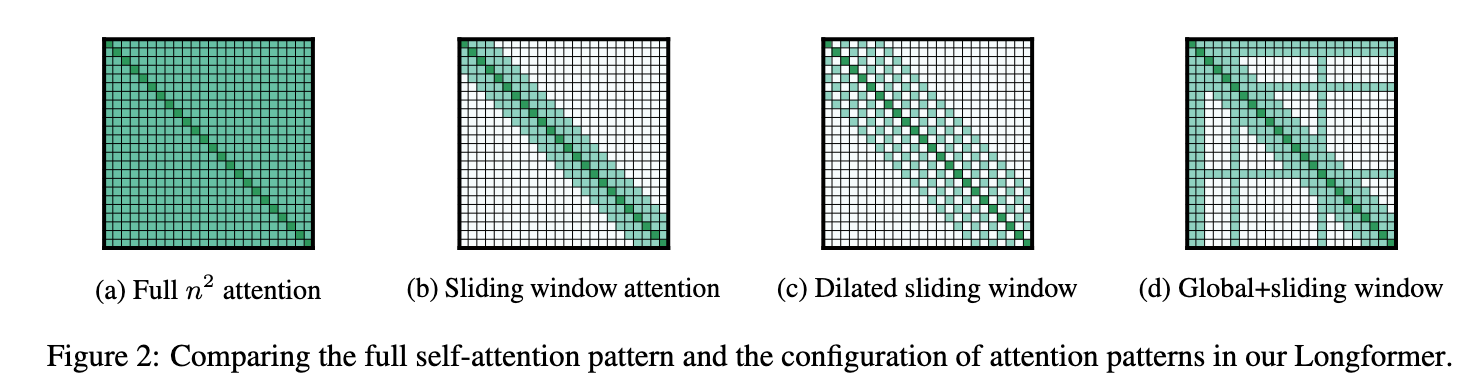
Pasted image 20251017134716.png
(Image taken from [1])

The authors used smaller window sizes in lower layers and larger ones for later layers, allowing the early layers to learn local context and the later layers to learn high-level representations.

Dilation is not used in the lower layers but it is used to 2 heads in the later layers

BigBird

Introduced in [2]

Similar to Longformer, they have a set of global tokens attending to all parts of the sequence, and all the tokens attend to a set of $w$ local neighboring tokens.

Unlike Longformer, the authors makes sure that all the tokens attends to a set of $r$ random tokens.

The authors looked at the attention mechanism from a directed graph viewpoint. Each token is a node and there are directed edges from each node. If the graph is complete, it represents the usual self-attention.

The problem of reducing the attention complexity, could be seen as graph sparsification problem. According to graph theory, random graphs can approximate complete graphs. A class of random graphs called as small world graphs could model both the global graph properties and the context of local neighbours. To make sure to learn the context between distant tokens, the token randomly attends to $r$ tokens.(Note: I personally need to look into the graph theory. However, I am trusting what the authors claim in their paper)

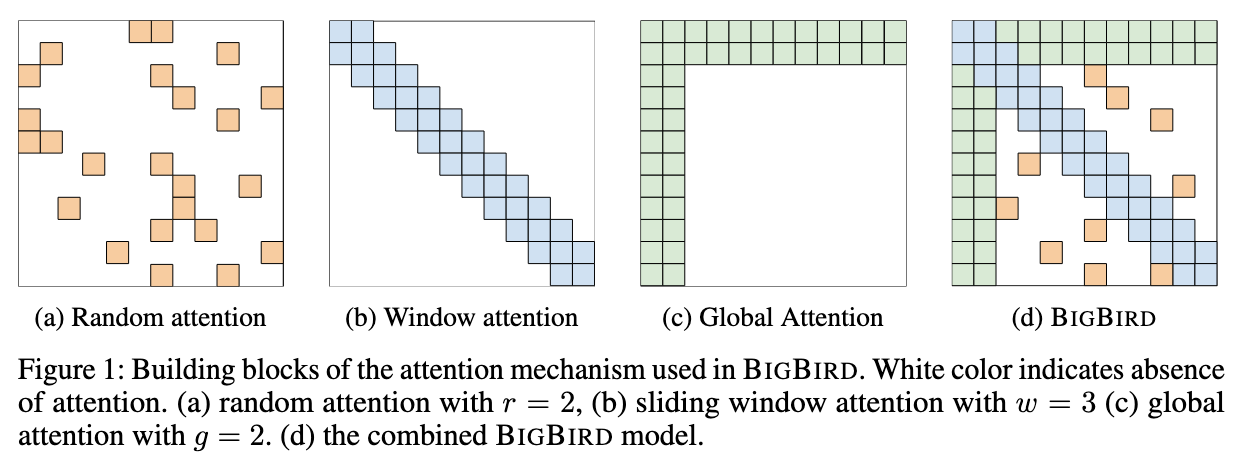
Pasted image 20251017141511.png
(Image taken from [2])

The global tokens can be from the existing tokens or they could also be additional added tokens.

The authors provide proof that their sparse attention mechanism used in full Transformers is also Turing Complete like that of the regular Transformers.

However, as we all know "There is no free lunch". For few tasks that could be solved by a single layer of the usual self-attention, Sparse Attention Mechanism might need polynomially more layers.

Aside from the addition of random tokens, there are a few more changes compared to Longformer

Both the global and local attention use relative position embedding while Longformer uses Absolute Positional Embeddings (There will be soon be an article about different positional embeddings)
During finetuning, the global tokens are trained using Contrastive Predictive Coding, a self-supervised learning framework using a contrastive loss called InfoNCE.

Reformer

Introduced in [3]

Improves the efficiency of standard transformer through replacing the standard dot product attention and reducing the memory needed by storing only the last activation for backprop instead of storing the activations for all the layers.

Standard Dot Product Attention is replaces with LSH Attention. The core idea is based on the softmax.

Softmax is dominated by the largest elements, so for a given query $q_{i}$ we could just consider the closest keys. Locality Sensitive Hashing can be used to find nearest neighbors in high-dimensional spaces.

A hashing scheme is locality-sensitive if nearby inputs gets the same hash with high probability and distant ones do not. The authors have used a hashing scheme based on angular projections.

Given input $x$ , to get $b$ hashes in total,

Take a Random Matrix $R$ of size $[d_{k}, b / 2]$
Concatenate $x R$ and $- x R$ to get $y$
Then $h (x) = a r g m a x (y)$

Once the tokens are assigned to specific hashes (hash buckets), then they are sorted based on the hash bucket. Then the whole sequence is chunked and each token is attend to tokens in their own hash bucket in their chunk and the previous chunk.
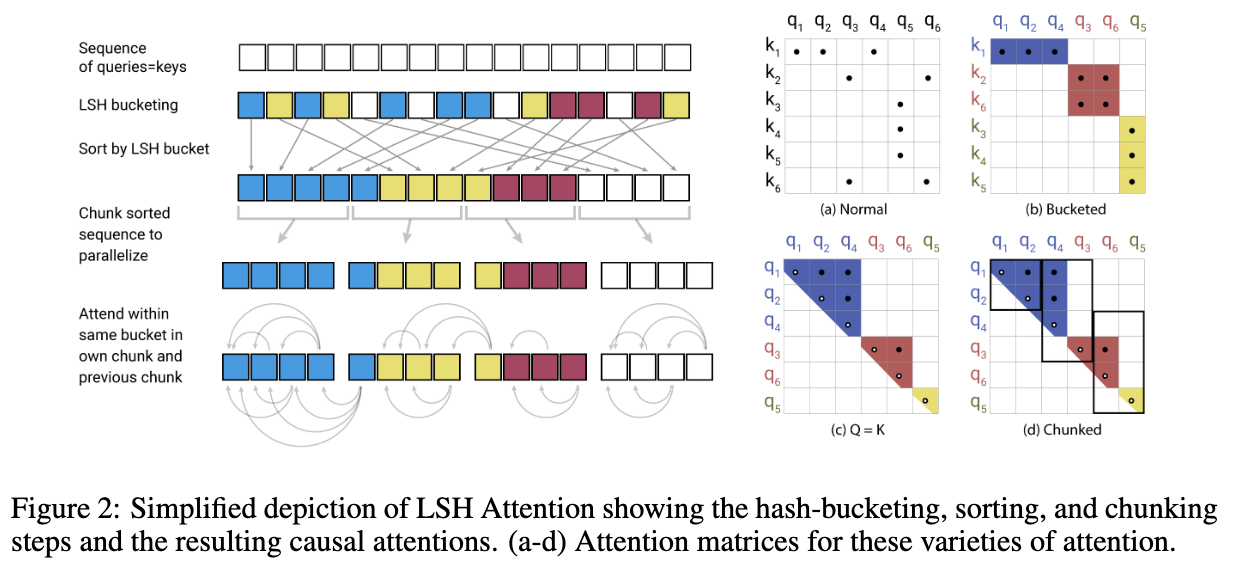
Pasted image 20251017192617.png
(Image taken from [3])

Sometimes when hashing, similar items could fall in different buckets. To reduce the probability of this happening, we could perform multiple rounds of LSH hashing with different hashing function and take the union of them. However, this reduces the efficiency gains

This reduces the complexity to $O (n l o g n)$

Linformer

Introduced in [4]

Aside from hashing and sparsity, low rank factorization has also been employed.
The original scaled dot product attention matrix is factorized into smaller attention matrices.

Through applying Singular Value Decomposition across different layers of pre-trained transformers, the authors saw that most of information of the context matrix is present in the first few largest singular values

The Key and Value Matrices are projected to $k$ dimension where $k <<< n$ . When $k = O (d / ϵ^{2})$ , the approximation error is $ϵ$ .
(Note: I need to look into the proof. It uses a lemma called Johnson-Lindenstrauss Lemma and I have no clue what is it. I will update the proof once I read about the lemma.)
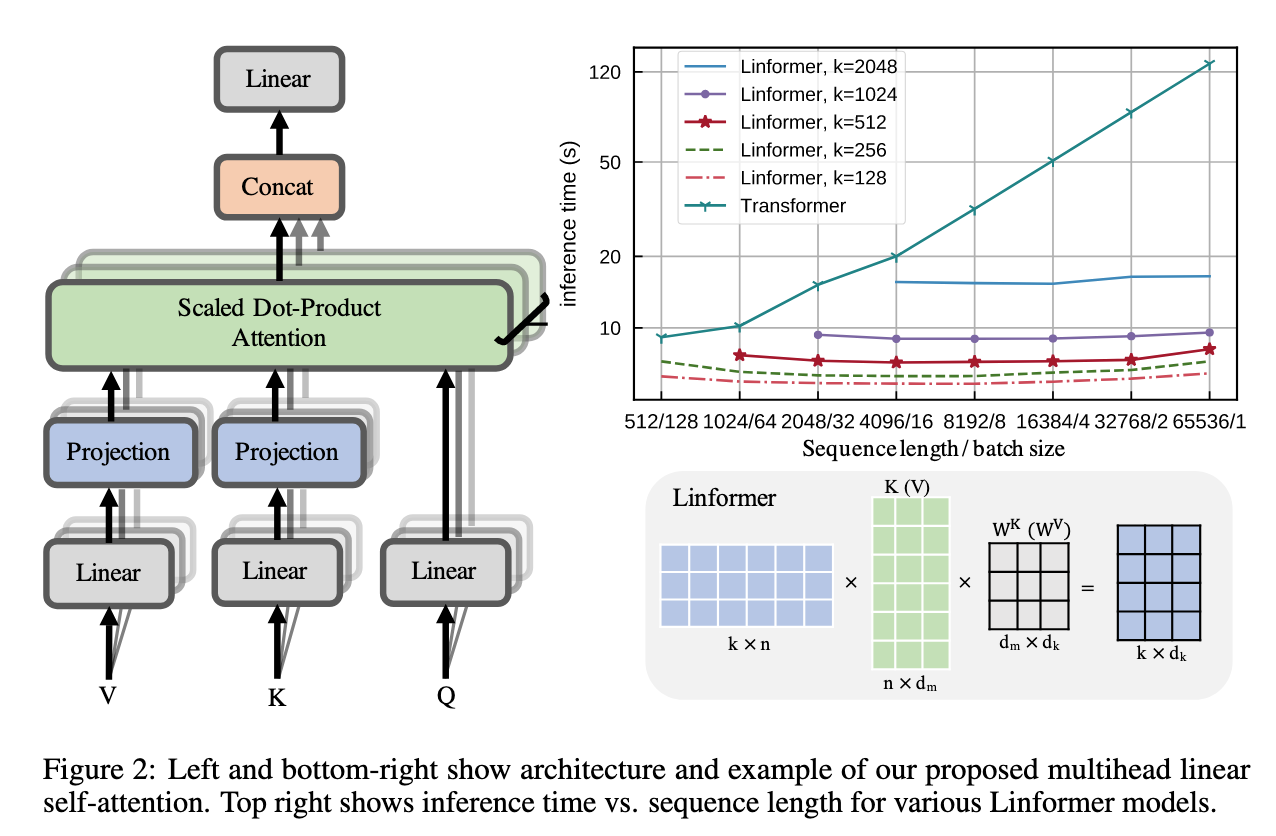
Pasted image 20251017200206.png
(Image taken from [4])

The authors have also shared the parameters at a lot of places. The projection matrix is shared across all heads. The Key and Value could also have the same projection matrix. The projection matrix could also be shared across all layers. They have found that just using a single projection matrix across all layers, heads gives the same as not sharing them at all.

The higher layers could use a smaller projected dimension than the early layers.

Performer

Introduced in [5]

Core Idea - Estimate Softmax Kernels with Positive Orthogonal Random Features.

It is called FAVOR+ mechanism, which stands for Fast Attention Via Postive Orthogonal Random Features. This allows them to have a time complexity of $O (L d^{2} l o g (d))$ where $L$ is the sequence length and $d$ is the dimension of the embedding

The authors propose a way to decompose the softmax in the traditional attention.
You could write the traditional attention as follows:

A t t e n t i o n (Q, K, V) = \frac{A V}{D}

A = e x p (Q K^{T} / \sqrt{d})

D = d i a g (A 1_{L})

$1_{L}$ is a vector of all ones of length $L$ .

The issue is computing. $A$ and the exponential can't be decomposed cleanly.

Let's say you have a way to transform $Q$ and $K$ into $Q^{'}$ and $K^{'}$ such that $$A \approx Q'K'$$
This allows us to multiply $K^{'}$ with $V$ then multiply with $Q^{'}$
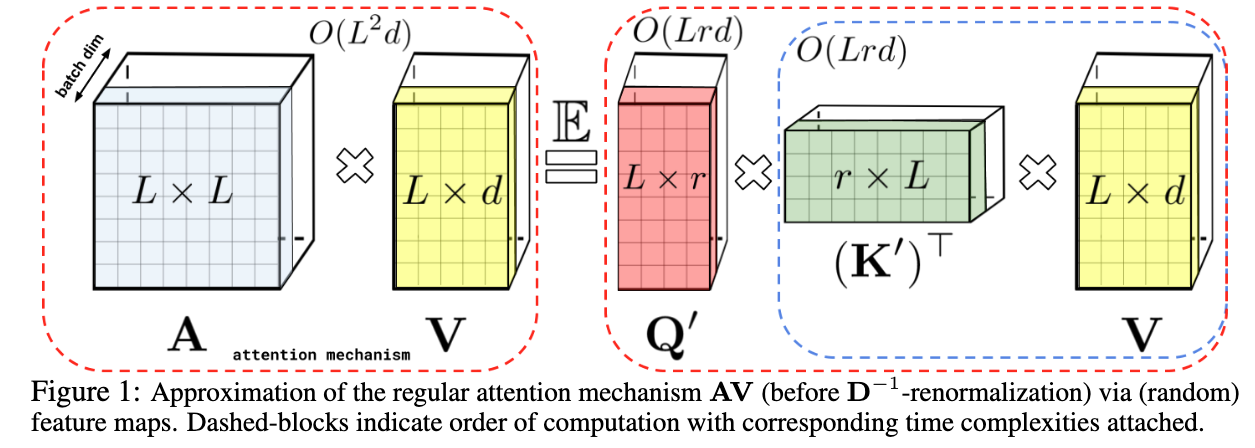
Pasted image 20251017203508.png
(Image taken from [5])

The authors claim that when passing the query and key matrices through function $ϕ (x)$ of the following form

ϕ (x) = \frac{h (x)}{\sqrt{(} m)} (f_{1} (w_{1}^{T} x), \dots, f_{1} (w_{m}^{T} x), \dots, f_{l} (w_{1}^{T} x), \dots, f_{l} (w_{m}^{T} x))

$w_{i}$ are deterministic vectors from a Distribution (Usually a Gaussian)

For softmax the approximation is done through the following parameters

h (x) = e x p (x y e a h $ $ $ $ l = 2

f_{1} = s i n

f_{2} = c o s

However, this approximation doesn't work around values around 0 and especially negative values. Therefore, they have found a better approximation which works for values close to 0 and less than 0.

They use the following parameters

h (x) = \frac{1}{\sqrt{2}} e x p (- \frac{| | x | |^{2}}{2})

l = 2

f_{1} (u) = e^{u}

f_{2} (u) = e^{- u}

The more $w$ you sample from the Gaussian, the better the approximation. It is even better if they are orthogonal to each other, so they use Gram-Schmidt Orthogonalization.

The Random Parameters need to be Redrawed after every step, otherwise they achieve the same performance of Linformer.

Current Era

Instead of Approximating, Flash Attention showed that a lot of time is wasted in moving data around the GPU SRAM and CPU HBM.

The current models use FlashAttention with optimizations applied for inference.
(There will soon be articles on this topic)

References

[1]

I. Beltagy, M. E. Peters, and A. Cohan, “Longformer: The Long-Document Transformer,” Dec. 02, 2020, arXiv: arXiv:2004.05150. doi: 10.48550/arXiv.2004.05150.

[2]

M. Zaheer et al., “Big Bird: Transformers for Longer Sequences,” Jan. 08, 2021, arXiv: arXiv:2007.14062. doi: 10.48550/arXiv.2007.14062.

[3]

N. Kitaev, Ł. Kaiser, and A. Levskaya, “Reformer: The Efficient Transformer,” Feb. 18, 2020, arXiv: arXiv:2001.04451. doi: 10.48550/arXiv.2001.04451.

[4]

S. Wang, B. Z. Li, M. Khabsa, H. Fang, and H. Ma, “Linformer: Self-Attention with Linear Complexity,” Jun. 14, 2020, arXiv: arXiv:2006.04768. doi: 10.48550/arXiv.2006.04768.

[5]

K. Choromanski et al., “Rethinking Attention with Performers,” Nov. 19, 2022, arXiv: arXiv:2009.14794. doi: 10.48550/arXiv.2009.14794.