DINO Series of Self-Supervised Vision Models

#CV #SSL #research/paper
DINO -> self DIstillation with NO labels.

Motivation behind DINO => Self-Supervised Pretraining in NLP was one of the main ingredients for success of Transformers in NLP. Image-Level Supervision reduces the rich concepts present in an image to a single concept, so we don't need any form of image-level supervision.

A few properties that emerge in Self-Supervised ViTs:

Features explicitly contain the scene layout and object boundaries.
Features perform well with a basic nearest neighbors classifier without any finetuning.

The second property only emerges when combining momentum encoder with multi-crop augmentation. Usage of small patches is also needed important to improve the quality of the resulting features.

DINO Approach

Architecture of DINO -

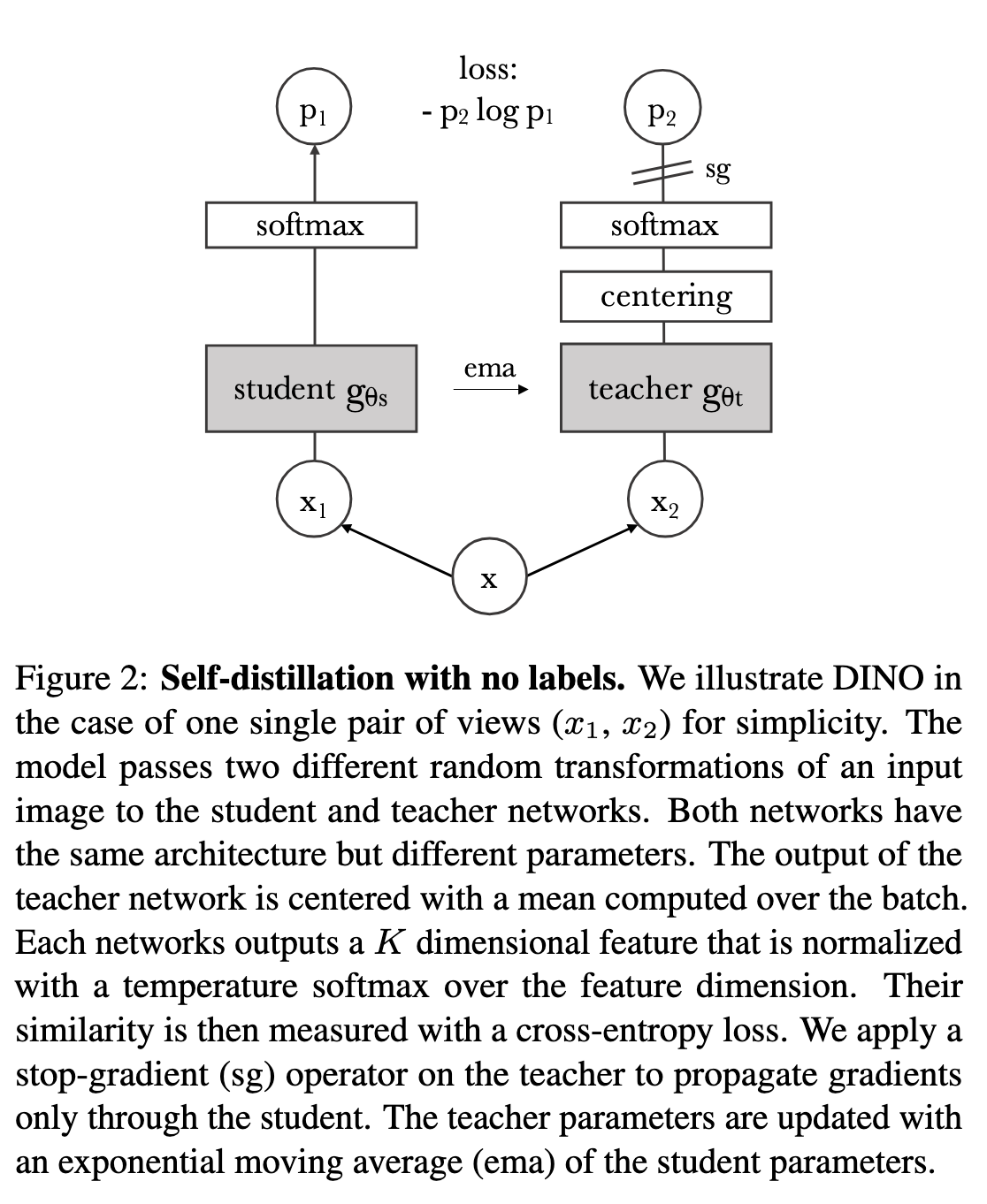
Source - Taken from [@caronEmergingPropertiesSelfSupervised2021]

The approach used in DINO is similar to Knowledge Distillation.

Knowledge Distillation

Student Network $g_{θ_{s}}$ learns to match the output of a given teacher network $g_{θ_{t}}$ , parameterized by $θ_{s}$ and $θ_{t}$ respectively. It is done through minimizing the cross-entropy loss w.r.t the parameters of the student network. $$min_{\theta_s}( -P_t(x)log P_s(x))$$
This method of learning a student network is adapted in the case of DINO.

Multi-Crop Strategy

The first step is to generate distorted views and crops of an input image.

From a given image, two global views $x_{1}^{g}$ and $x_{2}^{g}$ and several local views are generated. These views form the set $V$ . All crops are passed through the student network, while only the global views are passed through the teacher network. Thus we can elaborate the loss above as follows: $$min_{\theta_s} \sum_{x \in {x_1^g, x_2^g}} \sum_{x' \in V} (-P_t(x),P_s(x'))$$

Implementation Detail: 
2 Global views at 224*224 resolution
Local views at 96*96 resolution

Both the networks have the same architecture

Strategies to update the Teacher Network - Momentum Encoder

Copying the student weight to the Teacher network doesn't work.
However, using an exponential moving average of the student weights works well for the teacher network - Momentum Encoder

θ_{t} = λ θ_{t} + (1 - λ) θ_{s}

where $λ$ follows a cosine schedule.

Lambda goes from 0.996 to 1 during training.

This teacher has better performance than the student at all stages of training. (A Question to Ponder About -> Why is this the case?)

Network Architecture

Composed of a backbone (ViT or ResNet) and a projection head.

For downstream tasks, just use the output of the backbone.

Projection Head - 3 Layer MLP with hidden dim 2048, followed by l2 norm and a weight normalized fully connected layer.

ViT architectures do not use Batch Norm by default. Similarly no BN in the projection heads as well. (Another question to ponder -> Does it work with Batch Norm?)

Avoiding Collapse

Uses Centering and Sharpening of the momentum teacher outputs to avoid model collapse.

Centering prevents one dimension to dominate, but this encourages the model to just give a uniform distribution as it's output. Sharpening has the opposite effect.

Applying both, just balances their effects which is sufficient to avoid collapse in presence of a momentum teacher.

Centering

Adding a bias term $c$ from each of the logits. The center $c$ is updated with an exponential moving
average $$ g_t(x) = g_t(x) + c$$

c = m c + (1 - m) \frac{1}{B} \sum_{i = 1}^{B} g_{θ_{t}} (x_{i})

Sharpening

Use a temperature of less than 0 in softmax, such as 0.04.

A few implementation details

lr = 0.0005 * batchsize/256 .. It is ramped up to this value in the first 10 epochs.

After this, a Cosine schedule with a weight decay of 0.04 to 0.4 is used.

The Temperature is set to 0.1 in the linear warm-up and then 0.04 to 0.07 in the first 30 epochs.

Data augmentations - Color Jittering, Gaussian Blur, Solarization

Ablations in DINO

Patch Size

Smaller Patch Size - better performance but lesser throughput

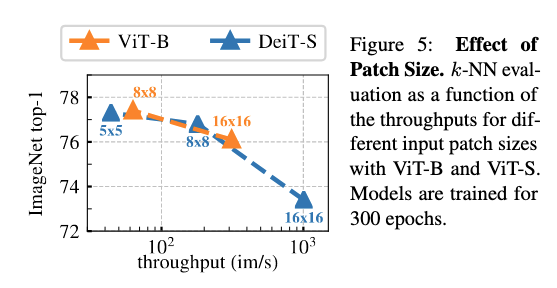
(Image taken from [@caronEmergingPropertiesSelfSupervised2021])

Teacher Network

Using the previous iteration copy of the student as teacher does not converge.
Using the previous epoch copy of the student as teacher converges and gives decent performance.
Momentum performs the best

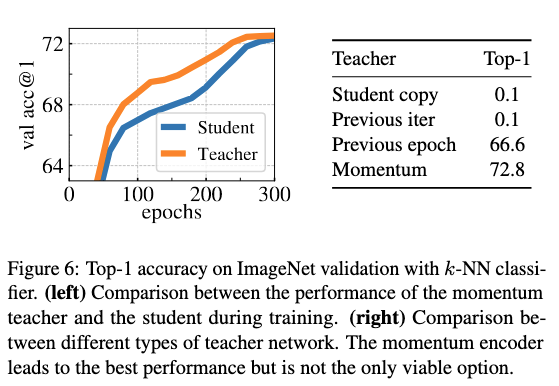
(Image taken from [@caronEmergingPropertiesSelfSupervised2021])

The Teacher outperforming the student at epochs only happens in the case of momentum encoder.

The authors propose to interpret the momentum teacher as some form of Polyak-Rupert Averaging. (This is something to dive into for another day.)

Batch Size

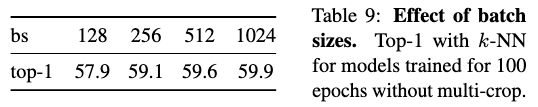
(Image taken from [@caronEmergingPropertiesSelfSupervised2021])

We can train excellent models by using small batch sizes as well.

References

[1]

M. Caron et al., “Emerging Properties in Self-Supervised Vision Transformers,” May 24, 2021, arXiv: arXiv:2104.14294. doi: 10.48550/arXiv.2104.14294.